开元棋官方正版下载 八下数学正方形最全知识点汇总

正方形是平行四边形中极为独特的一种，它兼具矩形的特性开元棋盘财神捕鱼官网版下载2023，也拥有菱形的特性，堪称四边形中的典范。

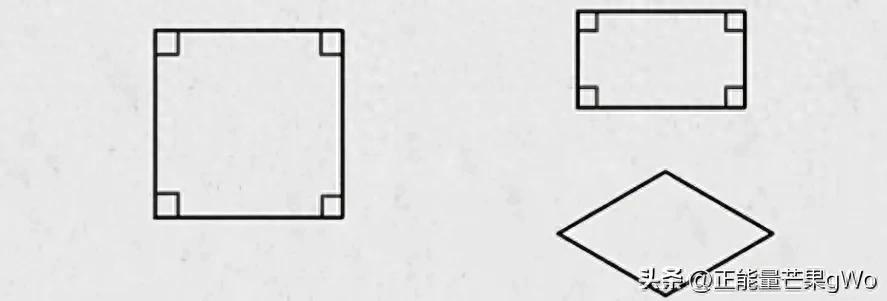
认识正方形

⒈正方形的性质。

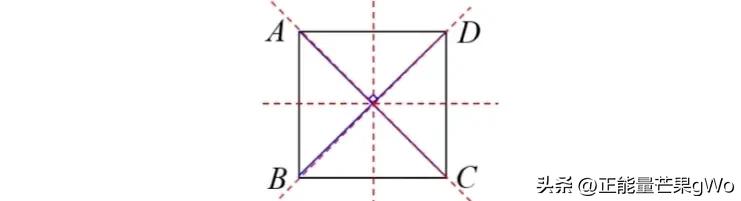
正方形的性质

正方形的四条边长度一致，两组相对的边相互平行，相邻的两条边相互垂直；正方形的四个内部角度都是九十度；正方形的两条对角线长度相等，并且它们相互垂直并且彼此平分，这两条对角线将正方形的四个内部角度均分，由这两条对角线分割出的四个小三角形都是等腰直角三角形；正方形具有轴对称性，通过两组相对边的中点的直线是其中的两条对称轴，而两条对角线则是另外两条对称轴。正方形属于中心对称图形，它有四条对称轴开元棋盘app官方版下载_开元棋盘app官网版下载-跑跑车，这些轴彼此交汇于一个点，这个点就是正方形的中心对称点。

正方形可以通过以下方式确定：一个矩形如果有一对相邻的边长度相同，那么它就是正方形；如果一个矩形的两条对角线互相垂直，那么它就是正方形；一个菱形如果有一个内角是直角，那么它就是正方形；一个菱形如果它的两条对角线长度相等开元ky888棋牌官网版，那么它就是正方形。

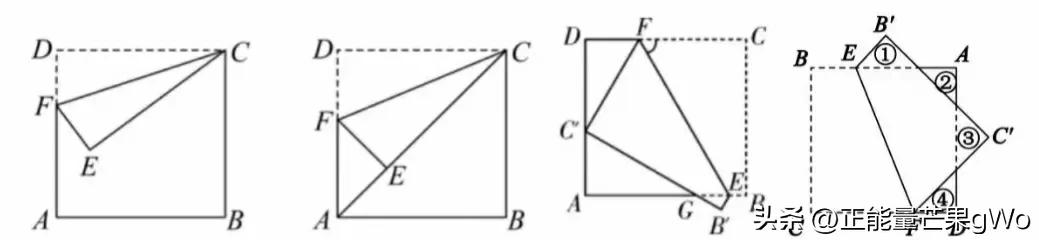
正方形翻折模型

正方形是历年中考中经常出现的题目类型，涉及正方形的几何图形种类丰富，包括平行线与中点组合的图形、正方形折叠形成的图形、手拉手形状的图形、一条直线上三个互相垂直的图形、正方形半角构成的图形、婆罗摩笈多图形、对角线互补的图形、正方形十字架形状的图形等。

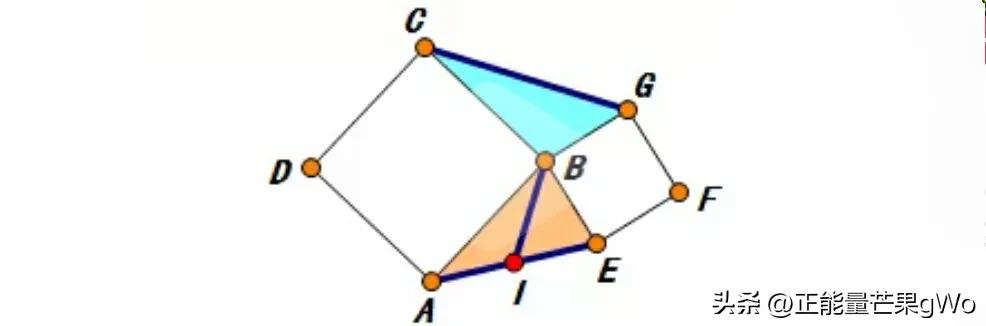
婆罗摩笈多模型

还会结合将军饮马、圆的相关知识点等进行考察，综合性很强。

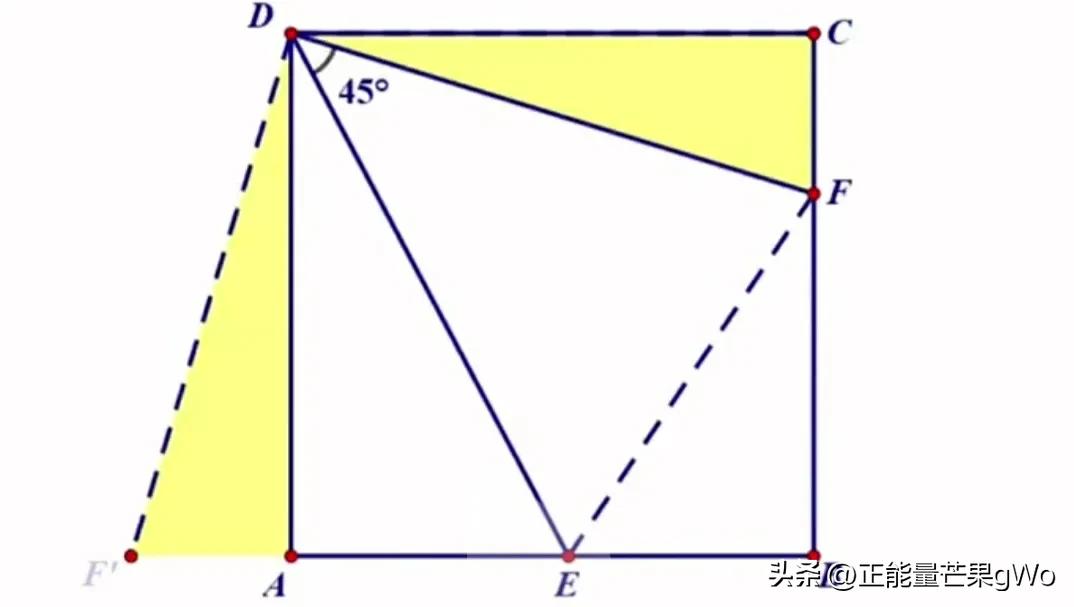
正方形半角模型

先前在论述全等三角形范例时，提及了部分范例，现在将着重阐释那些未曾涉及过的范例。

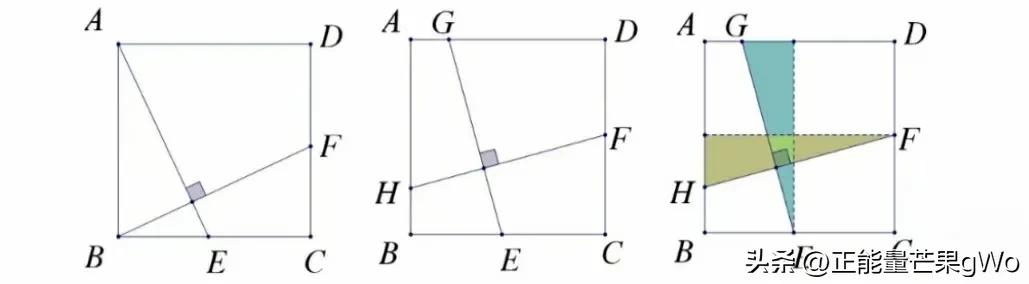
正方形十字架模型

⒊正方形的十字架模型。

正方形十字架基础模型条件是，当正方形有两条线段连接其两个顶点，并且这两条线段互相垂直时，就可以判定为十字架模型。

基础模型的证明过程十分简便，依据正方形具备的特性，能够确立判定三角形全等的两个标准，接着再确立一个相等的角，便完成了证明，无需赘述。至于非基础的十字架模型，则需要添加两条垂直于正方形边的辅助线，或者借助平移将其转化为基础模型，从而能够证明两个直角三角形全等。

正方形十字架形状的结论是，正方形内部有两条垂直的线段，那么这两条线段必定长度相等。但是，如果知道两条线段长度相等，并不能确定这两条线段一定垂直。

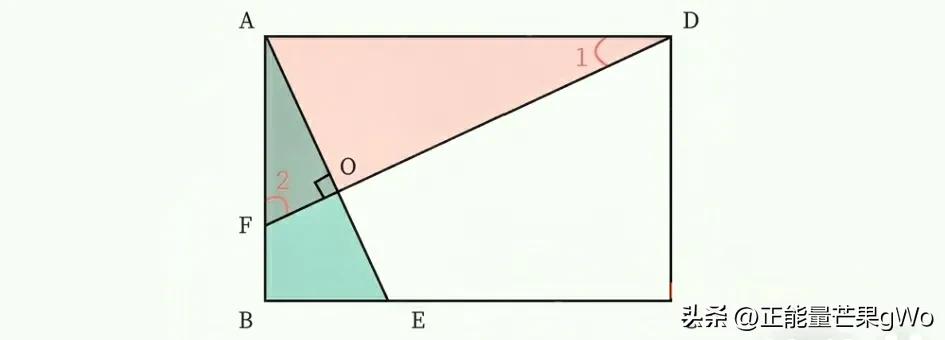
矩形十字架

十字架模型放入矩形后能产生相似三角形，矩形内两条互相垂直的线段，其长度之比等于矩形的长度与宽度之比。

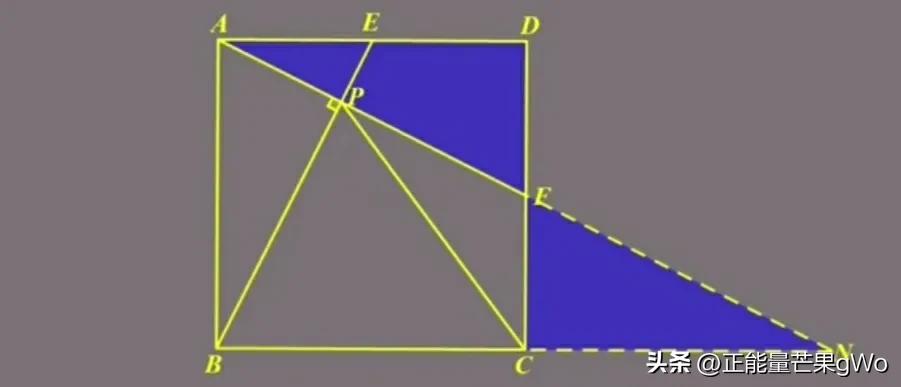
例题

如图所示，正方形ABCD具备特定属性，E点位于AD边的中点位置，F点位于DC边的中点位置，BE与AF两条线段存在交点P，PC连接起来，可以推测∠CBP与∠CPB之间可能存在某种角度关系。

这个题目没有直接给出BE垂直于AF这个条件，借助BAE和ADF全等的关系，可以推断出BE垂直于AF。然后利用平行线和其中点所形成的模型，可以构造出两个全等的三角形ADE和ECN，由此可以确定C是BN的中点。最后应用直角三角形斜边上的中线性质，能够得出PC等于BC。

正方形的各种几何关系，并非独立存在，一个题目常常需要结合好几个关系来求解，希望同学们能够精通这些关系，并且牢记它们各自的特点。